Hierarchy of Projections

Perspective Projections | OpenGL

Perspective Projections

1. The visual effect of the perspective projection is similar to the human visual system known as perspective foreshortening i.e. the size of perspective projection object varies inversely with the distance of the object from COP.



2. Perspective projection does not preserve parallel lines.


3. Vanishing Point
Any set of parallel lines that are not parallel to projection plan appear to converge to a point called vanishing point.

* In this case lines parallel to x and y do not converge, only lines parallel to z do so

* One point perspective projection of a cube

* A two point perspective projection of a cube

Parallel Projections | OpenGL

Parallel Projections

In case of parallel projection instead of having COP we have direction of projection (DOP), so the perspective projection whose COP is at infinity becomes parallel projection.
In parallel projections, the lines projecting from an object onto the image plane are parallel.
Two parallel projection systems:
1. Orthographic projection

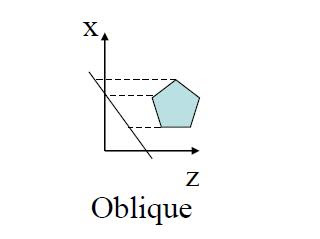
2. Oblique projection

In these the projection plane is normal and direction of projection differ.

Its major types are:
– Cabinet
– Cavalier

Projections

Projection
             Projection is the change in coordinate system and that is usually from 3D to 2D.

Projectors
             The projection of a 3D object is described by straight `projection rays' (called projectors).
Types Of Projection 

Projections can be divided into two basic
types
1. Perspective
2. Parallel
• The distinction between two is on the relation of COP and projection plane.
• If distance of one projector to another is finite then it is perspective projection otherwise it is parallel.


Perspective Projection

Parallel Projection

Viewing in Computer Graphics

Viewing in Computer Graphics

Viewing refers to positioning the camera in a coordinate frame and projection of the 3D object onto the 2D image plane of the camera.

Transformations Change Coordinate Systems

Transformations Change Coordinate Systems


One useful coordinate system transformation is given by:

Which transforms from a left handed to a right handed coordinate systems (and is its own inverse)

3D Homogenous Transformations

3D Homogenous Transformations
1. Rotation about x-axis

2. Rotation about y-axis

3. General form of a composition of transformations

3D Homogenous Transformations

1. Translation

 

2. Scaling

3. Rotation

Rotation Direction

Which way is +ive rotation

1. Look in –ve direction (into +ve arrow)

2. Counter Clock Wise is +ve rotation

3D Coordinate Systems | OpenGL

1. Right hand coordinate system

2. Left hand coordinate system(

Not used in OpenGL)

Composing Transformation

Applying several transforms in succession to form one overall transformation is known as Composing Transformation.

(M3 x (M2 x (M1 x P ))) = M3 x M2 x M1 x P

1. Transformation products may not be commutative.

    A x B != B x A

2. Some cases where A x B = B x A

 A                                    B

translation                        translation

scaling                             scaling

rotation                            rotation

uniform scaling                  rotation

(sx = sy)

3. Rotation and translation are not commutative.

Example :

Suppose we wish to reduce the square in the following image to half its size and rotate it by 45° about point P.

We need to remember that that scaling and rotation takes place with respect to the origin.

1– Translate square so that the point around which the rotation is to occur is at the origin

2– Scale

3– Rotate

4– Translate origin back to position P

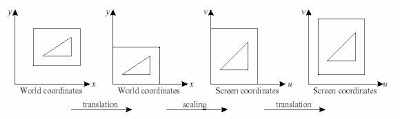
Window to Viewport Transformation

To display the appropriate images on the screen (or other device) it is necessary to map from world coordinates to screen or device coordinates.



This transformation is known as the window to viewport transformation, the mapping from the world coordinate window to the viewport (which is given in screen coordinates)

In general the window to viewport transformation will involve a scaling and translation as in figure below here the scaling in non-uniform (the vertical axis has been stretched).