Polygon Meshes- Important Steps

When working with polygon meshes, it is important to ensure that the mesh representation is consistent.

– All polygons are closed.

– Each edge is used at least once and not more than twice.

– Each vertex is referenced by at least two edges

Polygon Meshes - Pointers to an edge list

Polygon Meshes - Pointers to a vertex list

Polygon Meshes

A polygon mesh is a set of bounded polygons (vertices, edges, and faces) such that each edge is shared by at most 2 polygons

Polygon meshes can be represented in several ways

– Explicit representation

   P={(x1,y1,z1),........,(xn,yn,zn)}

Surface Modeling | Graphics Designing

Surface Modeling

Several methods are available to model surfaces

 

– Polygon meshes
• Surface is represented as a set of bounded planar surfaces
– Parametric polynomial curves
• Surface is defined by 3 equation in a parameter, t, one for each principal axis (x, y, z)

– Parametric bivariate polynomial surface patches
• Similar to parametric polynomial curves but this time each equation has two variables
– Quadratic surfaces
• Surface is implicitly defined by an equation f(x, y, z) = 0

Yaw, Pitch and Roll

In flight simulators, the angles of rotation are about the center of mass of the airplane. The camera is in the nose of the plane.

 Pitch :

 Roll :

 Yaw :

The U-V-N System

The camera plane is defined by 3 parameters:

• View Reference Point (VRP): A point (in the world frame) indicating the center of the camera's image plane. This specifies the position of the camera in space.
• View Plane Normal (VPN): A unit vector perpendicular to the camera's image plane. This specifies the orientation of the camera.
• View Up (VUP): A vector indicating the up direction (in world coordinates) for the camera.

3d Viewing in Computer Graphics

3d Viewing in Computer Graphics

      Two stages to the 3D to 2D transformation

• First a clipping,
• Then a projection.

The view volume of a perspective projection is the infinite volume defined by the combination of the PRP and the view window, which defines a pyramid. This can be contrasted to the view volume for a parallel projection which gives an infinite parallelepiped.

Projection Matrices

Hierarchy of Projections

Perspective Projections | OpenGL

Perspective Projections

1. The visual effect of the perspective projection is similar to the human visual system known as perspective foreshortening i.e. the size of perspective projection object varies inversely with the distance of the object from COP.



2. Perspective projection does not preserve parallel lines.


3. Vanishing Point
Any set of parallel lines that are not parallel to projection plan appear to converge to a point called vanishing point.

* In this case lines parallel to x and y do not converge, only lines parallel to z do so

* One point perspective projection of a cube

* A two point perspective projection of a cube

Parallel Projections | OpenGL

Parallel Projections

In case of parallel projection instead of having COP we have direction of projection (DOP), so the perspective projection whose COP is at infinity becomes parallel projection.
In parallel projections, the lines projecting from an object onto the image plane are parallel.
Two parallel projection systems:
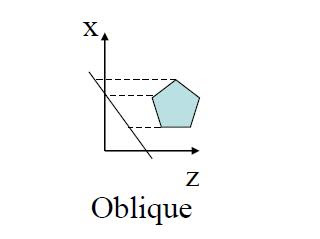
1. Orthographic projection

2. Oblique projection

In these the projection plane is normal and direction of projection differ.

Its major types are:
– Cabinet
– Cavalier

Projections

Projection
             Projection is the change in coordinate system and that is usually from 3D to 2D.

Projectors
             The projection of a 3D object is described by straight `projection rays' (called projectors).
Types Of Projection 

Projections can be divided into two basic
types
1. Perspective
2. Parallel
• The distinction between two is on the relation of COP and projection plane.
• If distance of one projector to another is finite then it is perspective projection otherwise it is parallel.


Perspective Projection

Parallel Projection

Viewing in Computer Graphics

Viewing in Computer Graphics

Viewing refers to positioning the camera in a coordinate frame and projection of the 3D object onto the 2D image plane of the camera.

Transformations Change Coordinate Systems

Transformations Change Coordinate Systems


One useful coordinate system transformation is given by:

Which transforms from a left handed to a right handed coordinate systems (and is its own inverse)

3D Homogenous Transformations

3D Homogenous Transformations
1. Rotation about x-axis

2. Rotation about y-axis

3. General form of a composition of transformations

3D Homogenous Transformations

1. Translation

 

2. Scaling

3. Rotation

Rotation Direction

Which way is +ive rotation

1. Look in –ve direction (into +ve arrow)

2. Counter Clock Wise is +ve rotation

3D Coordinate Systems | OpenGL

1. Right hand coordinate system

2. Left hand coordinate system(

Not used in OpenGL)

Composing Transformation

Applying several transforms in succession to form one overall transformation is known as Composing Transformation.

(M3 x (M2 x (M1 x P ))) = M3 x M2 x M1 x P

1. Transformation products may not be commutative.

    A x B != B x A

2. Some cases where A x B = B x A

 A                                    B

translation                        translation

scaling                             scaling

rotation                            rotation

uniform scaling                  rotation

(sx = sy)

3. Rotation and translation are not commutative.

Example :

Suppose we wish to reduce the square in the following image to half its size and rotate it by 45° about point P.

We need to remember that that scaling and rotation takes place with respect to the origin.

1– Translate square so that the point around which the rotation is to occur is at the origin

2– Scale

3– Rotate

4– Translate origin back to position P

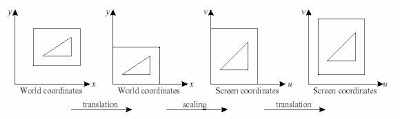
Window to Viewport Transformation

To display the appropriate images on the screen (or other device) it is necessary to map from world coordinates to screen or device coordinates.



This transformation is known as the window to viewport transformation, the mapping from the world coordinate window to the viewport (which is given in screen coordinates)

In general the window to viewport transformation will involve a scaling and translation as in figure below here the scaling in non-uniform (the vertical axis has been stretched).

Computer Graphics and Geometric Transformations

2D Transformations
2D computer graphics is the computer-based generation of digital images—mostly from two-dimensional models.There are three types of transformations that are essential in computer graphics

1-Translation
Moving an object to a new location by adding to objects x and y co-ordinates.
2-Scaling
Changing the size of the object.This can be uniform where both dimensions are re-sized by same factor or non-uniform.
3-Rotation
Object is rotated around the origin by specified angle.

Homogeneous Transformations
In order to represent a translation as a matrix operation we use 3 x 3 matrices and pad our points to become 1 x 3 matrices.

A program (Objects, Lights, Camera)

Lighting

1. Direction light source
2. Position light source
3. glLightfv( Light#, Attribute, …)
4. GLfloat position[] = {10, 10, 10, W} glLightfv(GL_LIGHT0, GL_POSITION, position) If (W) is zero the position is treated as a direction (a 1x3 vector); otherwise, it is treated as a position (a 1x4 vector)
5. glEnable(GL_LIGTHING)
6. glEnable(GL_LIGHT0)

Drawing in 3D

 Depth buffer
   Allows scene to remove hidden surfaces. Use glEnable(GL_DEPTH_TEST) to enable it.
   1-glPolygonMode( Face, Mode )
       Face: GL_FRONT, GL_BACK, GL_FRONT_AND_BACK
      Mode: GL_LINE, GL_POINT, GL_FILL
  2-glCullFace( Mode )
      Mode: GL_FRONT, GL_BACK, GL_FRONT_AND_BACK
  3-glFrontFace( Vertex_Ordering )
      Vertex Ordering: GL_CW or GL_CCW

OpenGL States

On/off (e.g., depth buffer test)

1. glEnable( GLenum )
2. glDisable( GLenum )
3. Examples:
4. glEnable(GL_DEPTH_TEST);
5. glDisable(GL_LIGHTING);

Mode States

1. Once the mode is set the effect stays until reset

     Examples:
    glShadeModel(GL_FLAT) or glShadeModel(GL_SMOOTH)
    glLightModel(…) etc.

OpenGL Primitives

Drawing two lines
glBegin(GL_LINES);
    glVertex3f(_,_,_); // start point of line 1
    glVertex3f(_,_,_); // end point of line 1
    glVertex3f(_,_,_); // start point of line 2
    glVertex3f(_,_,_); // end point of line 2
glEnd();
We can replace GL_LINES with GL_POINTS, GL_LINELOOP, GL_POLYGON etc.

OpenGL Syntax

All functions have the form: gl*
1-glVertex3f() – 3 means that this function take three arguments, and f means that the type of those arguments is float.
2-glVertex2i() – 2 means that this function take two arguments, and i means that the type of those arguments is integer.
All variable types have the form: GL*
1-In OpenGL program it is better to use OpenGL variable types (portability)
2-GLfloat instead of float
3-Glint instead of int

OpenGL Order of Operations

Construct shapes 
1-Vertices
2-Edges
3-Polygons
Use OpenGL to:
1-Arrange shape in 3D (using transformations)
2-Select your vantage point (and perhaps lights)
3-Calculate color and texture properties of each object
4-Convert shapes into pixels on screen

Overview of an OpenGL Program

Main
1-Open window and configure frame buffer (using GLUT for example).
2-Initialize GL states and display (Double buffer, color mode, etc.).
Loop
1-Check for events
    a)if window event (resize, unhide, maximize etc.)
    b)modify the viewport and Redraw
    c)else if input event (keyboard and mouse etc.)
    d)handle the event (such as move the camera or change the state) and usually draw the scene
Redraw
1-Clear the screen (and buffers e.g., z-buffer)
2-Change states (if desired)
3-Render
4-Swap buffers (if double buffer)

OpenGL

A high-performance, window-system independent, software interface to graphics hardware.

GLUT (Provides and easy access to the underlying windowing system – creating windows and looking for mouse and keyboard events etc.)
GLU (Provides helper routines built on top of OpenGL rendering capabilities)

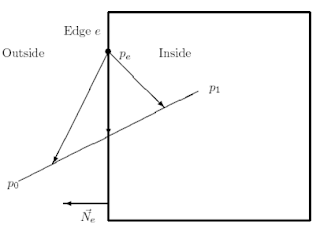
Sutherland-Hodgman Polygon Clipping

1-The Sutherland-Hodgman polygon clipping algorithm clips polygons against convex clipping windows.

2-It does so by clipping the subject polygon against each clip edge producing intermediate subject polygons.

3-The Sutherland-Hodgman may produce connecting lines that were not in the original polygon. When the subject polygon is concave (not convex) these connecting lines may be undesirable artifacts.

Polygon Clipping

Polygon clipping differs from line clipping in several respects:
1-The input to the clipper is a polygon, which for simplicity we will view as a list of n >= 3 vertices (v0; v1; : : : ; vn-1).
2-The output from the clipper is one or more polygons
3-The clipping process may generate vertices that do not lie on any of the edges of the original polygon.
4-Complex polygons (that is, non-convex) may lead to strange artifacts.

2D Clipping

Liang-Barsky 2D Clipping

Cohen Sutherland 2D Clipping

Cohen Sutherland 2D Clipping

2D Raster Algorithms

1-DDA Algorithm
The digital differential analyzer (DDA) samples the line at unit intervals in one coordinate corresponding integer values nearest the line path of the other coordinate.
Major deficiency in the above approach :
   1-Uses floats
   2-Has rounding operations

2-Bresenham’s Line drawing Algo
An accurate, efficient raster line drawing algorithm  developed by Bresenham, scan converts lines using only incremental integer calculations that can be adapted to display circles and other curves.

Display Primitives | Computer Graphics

Computer Graphics Display Primitives

1- Graphics (modeling & rendering) primitives
2- Points, lines, polygons
3- Various line-drawing algorithms
4- DDA and Mid-point Line Drawing Algorithms
5- Circles drawing
6- Mathematical concepts
      a)line equations
      b)parametric representation, implicit
7- Functions, vectors and matrices

Computer Graphics Design

Computer Graphics Design

Mechanism for video display
1-CRT principle and structure
2-Frame buffer
3-Dot size, resolution
4-Refresh rate
5-Shadow masking in colored CRTs
Logic structure for other display
1-LCD
2-Plasma display
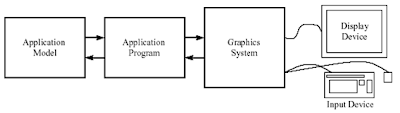
Conceptual Models for CG
1-Application Model
2-Application Program
3-Graphics System

I/O Devices
1-Printers and Plotters

Key Components of a Computer Graphics Design System

1-Video controller
2-Display processor